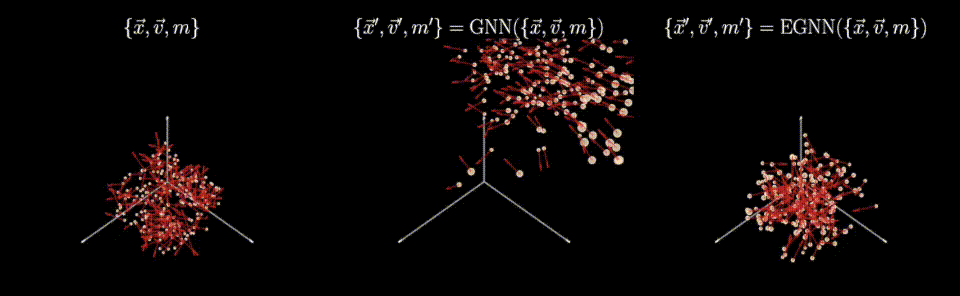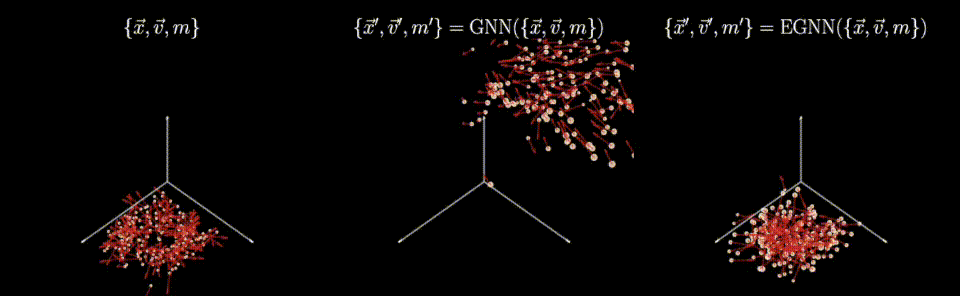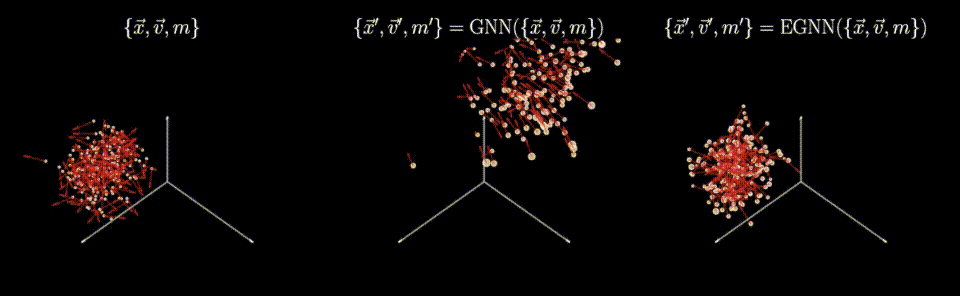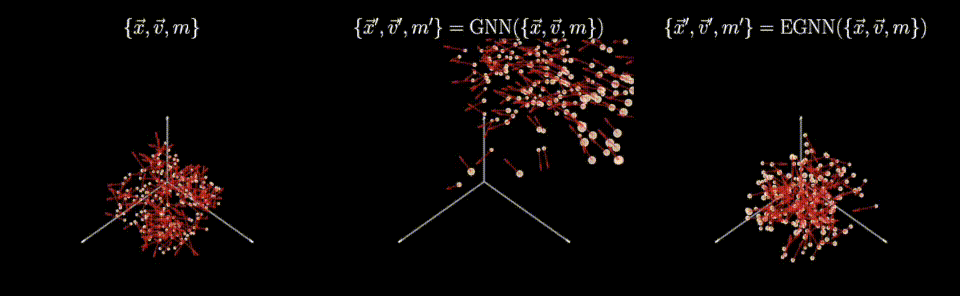The Unreasonable Effectiveness of Physics in AI

Physics keeps popping up in AI algorithms, and it’s not a coincidence.

Unreasonably effective?

Eugene Wigner famously stated that mathematics is unreasonably effective in the natural sciences. He noted that, “the enormous usefulness of mathematics in the natural sciences is something bordering on the mysterious and that there is no rational explanation for it”.

In machine learning and AI, it could similarly be argued that physics-based models are unreasonably effective. Foundational principles from thermodynamics and classical physics are routinely leveraged in modern AI and statistical learning algorithms such as diffusion generative models [1], Monte Carlo sampling methods based on Hamiltonian dynamics [2], and optimization algorithms inspired by physical annealing [3]. When referring to AI here, we note that we broadly encompass classical statistical algorithms in addition to, e.g., contemporary deep learning-based AI methods.

In this blog post, we will take a closer look into why there seems to be a mysterious synergy between physics and AI. Why are some of the more successful AI algorithms inspired by physics? Is this just a coincidence, or does it reveal a more profound, fundamental connection between the two?

Our main goals

It is clear that many modern AI models are not explicitly motivated by physics, such as transformers for language modeling (however, see here for a compelling connection). Hence, physics is clearly not necessary for performant AI. On the other hand, in many contexts, physics-based models are competitive with non physics-based ones, suggesting that physics may often be sufficient as a guiding principle. For example, state-space models, which were originally employed for control engineering, draw inspiration from physics and were recently shown to be competitive for language modeling [30]. Such sufficiency would nevertheless be compelling, since it motivates the development of highly physical approaches to AI algorithms with implications, e.g., for designing physics-based AI hardware. Thus, one goal of this blog is to highlight several examples where physics-based reasoning led to the development of new AI algorithms or new perspectives on existing algorithms.

The second goal is to provide explanations for why physical reasoning is often empirically helpful in providing high-level guiding principles for AI algorithm development. We will highlight features of physics-based models, such as continuity, interpretability, symmetry, and simplicity, which make them useful in certain real-world applications.

Some features of physics-based models

Simplicity as a feature

Occam’s razor: Physics-inspired models are often inherently simple and parsimonious, since physics is concerned with revealing simple universal truths; this has led to the description of physics as a “search for simplicity”. The simplicity of physics-based models is often considered a feature rather than a bug, which one can understand from the perspective of Occam’s razor: the guiding principle that advocates for seeking explanations constructed using the fewest possible components. The effectiveness of Occam's razor has been demonstrated time and again across various disciplines, as simpler explanations often prove to be more robust, reliable, and generalizable.

One can similarly apply Occam’s razor to machine learning models, where the goal is often to seek high-level explanations for seemingly complicated datasets that nevertheless generalize well. Physics-inspired modeling can therefore be viewed as an attempt to implicitly leverage Occam’s razor in the context of machine learning.

Caption: Natural data (left) is often embedded in a lower-dimensional manifold (right) in a structured but non-obvious way. Physics-grounded methods can be effective in unearthing this structure.

Low-dimensional manifolds: The manifold hypothesis [4] can be seen as a manifestation of Occam’s razor. The statement is that most natural datasets lie close to a low-dimensional manifold, which happens to be embedded in a higher dimensional space in a structured way. (See figure above where the data lie on a torus manifold embedded in 3D space.) The hypothesis alludes to the existence of simpler explanations of the data, waiting to be found.

In this context, the manifold hypothesis provides further motivation for physics-based models: physical laws give rise to low-dimensional manifolds of natural data, and physics-inspired models serve as powerful tools to effectively unearth explanations behind real-world datasets.

Smoothness as a feature

Mathematics is the Wild Wild West, where anything goes. Discontinuous and non-differentiable functions abound. In principle, one could search over the space of such pathological (colloquially speaking) functions during the learning process in the context of AI. 

Oftentimes, explicitly regularizing the learning process to prefer smooth, continuous function is desirable. Physics-based methods tend to be biased towards well-behaved functions since they have a correspondence to the natural world. Thus, choosing a model inspired by physics can be seen as applying an inductive bias to the statistical learning process, which can be useful for speeding up training and inference as well as improving the generalizability of models. Indeed, the smooth and well-behaved properties of physics-based models have recently been exploited to construct novel classes of physics-based generative AI models [5].

Symmetry and scale separation as features

As mentioned above, natural datasets often live in structured, low-dimensional manifolds. The use of physically-informed inductive biases can place powerful priors on the space of functions that AI models process, helping effectively break the curse of dimensionality associated with complex real-world data. Two such physics-informed inductive biases are symmetry and scale separation. Scale separation enforces a multi-scale, hierarchical structure ubiquitous in the real world, common examples being the pooling operation in convolutional neural networks and the philosophy behind wavelet-based approaches to data analysis.

Phil Anderson famously said that “it is only slightly overstating the case to say that physics is the study of symmetry”. Symmetry priors are used as guiding principles behind many neural network models today [11]. Convolutional neural networks, for example, naturally emerge through enforcing translational symmetry [12]. Another prominent example is AlphaFold 2, where the use of 3-D symmetry was instrumental to achieving its paradigm-shifting performance for protein structure prediction [13]. 

Physics-based inductive biases are especially useful when analyzing data from physical systems, and this has motivated neural networks based on Hamiltonian [14] and Lagrangian [15] dynamics. Taking this one step further, one can literally use a physical system as the neural network, as in deep physical neural networks [16]. All of these ideas can be exploited from an inductive bias perspective.

Caption: Symmetry-preserving models (right) can faithfully incorporate physical transformations of the data (left) unlike vanilla models (middle).

Interpretability as a feature

Interpretability is often a desirable feature of AI models. Since humans have strong intuition for physical systems, the parameters of a physics-based model can carry conceptual meaning. Closely related to the concept of symmetry priors above, restricting the nature of message passing in graph neural networks in a domain-specific manner can result in learning interpretable features, as in this example of learning the dynamics of gravitationally-bound multi-particle systems using symbolic expressions for message passing. Interpretability thus  provides another motivator for physics-based models, further highlighted in [6,7].

Besides feature interpretability, physics-based algorithms can also aid in model interpretability. Algorithms used to fit AI models frequently have complex behaviors and physics can be a key tool in understanding how they work. For instance, the physics-based intuition that adding momentum to a model will aid in exploration is born out in both the popular Nesterov-type extensions to stochastic gradient descent [31], and in the success of Hamiltonian Monte Carlo [2]. In the latter case, the simple physics-based intuition that the Hamiltonian should stay constant when generating a proposal leads to both an extremely effective algorithm for sampling from a general probability distribution, but also a natural model diagnostic (has the value of the Hamiltonian diverged from its initial value?) that can successfully indicate that your model has problematic features.

Dynamical modeling as a feature

Explicitly modeling the learning process as a continuous dynamical system opens up a range of new possibilities, such as leveraging powerful differential equation solvers and being able to effectively model continuous underlying latent processes. A canonical example is that of Neural Ordinary Differential Equations (Neural ODEs) [8], which introduced a class of AI models where a pass through the network involves a continuous transformation -- the network is explicitly modeled as a dynamical system (Figure below from [8]).

Caption: Neural ODEs can explicitly model neural networks as dynamical systems (from [8])

A key motivator was computational: differential equation solvers, which had been developed and fine-tuned over many decades, could be leveraged for much of the computational heavy lifting. Neural ODEs and their variants show promising performance on a variety of tasks across domains and enable principled inference for datasets that are challenging to analyze with traditional methods, such as irregularly-sampled time series.

Since physical processes are often governed by differential equations, neural ODEs encourage an analogy between neural networks and continuous-time, physical dynamical processes. This can allow for the discretization of the underlying differential equations in a way that can be used to efficiently realize neural networks at the hardware level.

A recent, related line of work explicitly re-interprets graph neural networks and associated learning processes as continuous dynamical systems inspired by physics. This provides deep insights into the nature of learning on graphs that are otherwise difficult to address with traditional graph frameworks by, e.g., drawing direct analogies between different types of GNNs and diffusion PDEs solved by specific numerical schemes.

Probabilistic nature a feature

Probabilistic machine learning [9] is becoming increasingly prevalent, given the need for principled uncertainty quantification across domains as well as the real-world impact of generative modeling over complex data distributions, from natural images to biomolecules. A probabilistic approach to AI allows for principled uncertainty quantification and increases the reliability and trustworthiness of the model’s predictions while leveraging powerful concepts from traditional statistical inference, such as latent variable modeling.

Caption: Probabilistic methods (here: Gaussian processes) can effectively model distributions over quantities of interest, including uncertainties.

Not surprisingly, the field of probabilistic AI in particular has benefitted from many physics-inspired models (some of which we discuss below). This is partly because probabilistic reasoning is prevalent in physics, especially in statistical mechanics, thermodynamics, and quantum mechanics. These subfields of physics therefore offer both intuition and formal frameworks for formulating models for probabilistic AI.

Examples of physics-inspired models

Having outlined several features of physics-based approaches, let us highlight some key examples where these approaches have yielded powerful AI and statistical learning algorithms in practice.

Energy-based models

It may be evident, but energy-based models (EBMs) [19] draw substantial inspiration from physics. Specifically, Hopfield networks and Boltzmann machines were originally inspired by spin-glass models, which are Ising spin models with random couplings. EBMs like Boltzmann machines can be used for sampling  in generative AI applications, highlighting a more general trend of physics-based being especially useful for generative AI.

Diffusion models

Perhaps more than any other model, diffusion models [1] embody the spirit of this message: they are probabilistic, they are continuous in time [21], and of course, they are physics-inspired. Originally inspired by non-equilibrium thermodynamics [1], diffusion models incorporate noise into the learning process, effectively smoothing the distribution to facilitate learning. This is particularly useful given the manifold hypothesis (see above), which suggests that learning natural data distributions would be challenging due to their complex structure.

Caption: Diffusion models are a class of physics-inspired generative models that can learn to iteratively generate complex data starting from noise.

Samples are then drawn by reversing the diffusion process, providing a state-of-the-art algorithm for generative AI that is used for applications including molecular docking [22], protein folding [23], and crystal design [24]. Recently, the connection to physics has been pushed even further [5], extending the generative AI paradigm to other physics-inspired models such as the Poisson equation in electrostatics.

Markov Chain Monte Carlo

In probabilistic AI and Bayesian inference more broadly, Markov chain Monte Carlo (MCMC) [25] is a workhorse for various learning tasks. The history of sampling algorithms like MCMC is closely intertwined with physics. The modern version of Markov Chain Monte Carlo was invented at Los Alamos in the 1940s by Stanisław Ulam while studying neutron diffusion in nuclear weapon cores, and further fleshed out in work with John von Neumann and Nicholas Metropolis. 

An important criterion in MCMC is detailed balance, connected to the invertibility of the sampling proposal distribution. Physics yields simple and elegant ways to enforce detailed balance, e.g. through energy conservation. Inspiration from physics has continued to yield rich classes of techniques for both optimization and sampling in recent years.

Hamiltonian Monte Carlo: A state-of-the-art MCMC algorithm is Hamiltonian Monte Carlo (HMC), which is based on introducing an auxiliary variable (“momentum”) and evolving particles in time according to Hamiltonian dynamics [2]. These dynamics, which stem from classical mechanics and are intimately related to the principles governing the motion of physical systems, facilitate inference by proposing samples that effectively explore the parameter space in a much more efficient manner than traditional MCMC algorithms like Metropolis-Hastings-Rosenbluth (Figure below).

Caption: Sampling algorithms based on Hamiltonian dynamics (top) can sample complex distributions much more efficiently than traditional MCMC methods (bottom).

Bolstering the theme of physics roots for sampling techniques, HMC (also known as Hybrid Monte Carlo) was originally proposed in the late 1980s in the context of studying lattice chromodynamics, a theoretical framework for describing the strong nuclear force that binds quarks and gluons together into protons, neutrons, and other particles.

Stochastic gradient HMC: Diving deeper, there is an esoteric but useful MCMC algorithm called stochastic gradient Hamiltonian Monte Carlo (SGHMC) [26]. Here, noisy estimates of the gradient are employed, which introduces stochastic fluctuations into the dynamics. These fluctuations are undesirable: they perturb the dynamics, and to deal with this dissipation was introduced into the equations to damp out the noise. In this case, fluctuations alone were detrimental, but combining fluctuations with dissipation leads to good properties in the solution. 

Intriguingly there is a theorem in thermodynamics called the fluctuation-dissipation theorem, which is typical of say Brownian motion, stating that fluctuations and dissipation always go hand-in-hand, like two peas in a pod. So it could be argued that the SGHMC algorithm is physics inspired, and in particular thermodynamics inspired.

Variational inference algorithms

Variational inference is a complementary method to MCMC for approximating complex posterior distributions, turning posterior inference into an optimization rather than sampling problem. Instead of trying to compute a complex distribution directly, the method defines a simpler, typically parameterized family of distributions, and then finds the member of that family which is closest to the target distribution.

There is a direct analogy with variational methods from quantum mechanics, where the idea is to find variational approximations to ground state wavefunctions of a system by minimizing the expectation value of the energy. On a historic note, exploiting the connection Ising models and Boltzmann machines initially introduced variational methods to the field of AI in the late 1980s, which are a cornerstone of today's probabilistic AI toolkit; see here for a deeper exploration of this connection.

Caveats

Now that we have presented some arguments and examples, in the spirit of steelmanning let us offer some caveats, to the skeptics out there, regarding the connection between physics and AI.

Historical and psychological effects

Since the field of physics was developed before AI, it could be argued that historical effects play a role. Indeed, physics has a long history even before the term AI was coined in 1955. As a result, researchers may be using their past experience in physics as their starting point for how to formulate models in AI. Moreover, human psychology plays a role: we have great intuition for physical processes since we interact with the physical world. Hence, our own intuition lends itself to physics-based modeling..

Is math the intermediary?

The fundamental underpinnings of both physics and AI are naturally formulated in the language of mathematics, including concepts from geometry, linear algebra, and information theory. Perhaps it is their mutual connection to these subfields of mathematics that effectively connects physics and AI?

When it comes to statistical learning, we are usually still grounded in the natural world, relying on concepts like geometric data types (scalars, vectors, tensors, …) and probability densities—even if we work with abstract models that obfuscate this connection. It may therefore not be entirely surprising if concepts that are ubiquitous in formulating physical principles, like geometry and linear algebra, work well in the realm of inference.

Similarly, the concept of entropy shows up in a central way in both thermodynamics and machine learning. But it could be argued that this is because both thermodynamics and machine learning are mutually connected to a third field: information theory, a mathematical framework for quantifying and propagating information. One can see how machine learning is connected to information theory since, e.g., data compression, latent variable modeling, and the information bottleneck are central concepts here. Hence, the unifying language of information theory happens to be a useful lens for both physics and machine learning.

A good starting point?

Physics-based models are clearly effective for building inference strategies. However, they may be most effective as starting points, with engineering and practical considerations taking over at some point. For example, Hamiltonian Monte Carlo is notoriously hard to tune in many cases, with domain- and problem-specific engineering and insight often needed to get it working well.

The above image was generated by the text-to-image diffusion model Midjourney, and hence diffusion models are clearly useful! The diffusion process in these models gives one way to destroy and create information, but there are many others, some physics-based (e.g. based on electrostatics), some not really (e.g. cold diffusion). The jury is still out on which types of models will strike a good balance in the end between all the relevant axes. 

There is clearly something very fundamental in why physics-based models work well for statistical inference and for AI. But they may be best as starting points and as ways to guide strategies for building models -- otherwise one could get stuck in a local minimum. However new physics-based strategies often lead to qualitative leaps in performance and understanding, providing fundamental breakthroughs at the conceptual level.

Hardware Implications

While algorithmic developers have been quick to pick up on the connection between physics and AI, the implications for designing AI hardware have not been fully appreciated. All computing hardware naturally obeys the laws of physics, including digital hardware. But in theory one could exploit the laws of physics more directly with analog hardware, where physical evolution is exploited as part of the computation. We therefore leave the intriguing question open: how can one exploit the aforementioned connections between physics and AI to better design AI hardware? Some recent work along these lines includes probabilistic hardware with p-bits [27,28] and thermodynamic hardware with stochastic units coupled to an entropy regulator [29], both of which have applications for probabilistic AI and generative AI.

Conclusion

In summary, we highlighted several positive features of physics-inspired models that make them a good fit for use in AI.

• Their parsimonious nature allows for an elegant trade off between expressivity and simplicity;

• Incorporating domain-specific parameterization can allow for greater interpretability of physics-based models;

• They allow one to naturally incorporate inductive biases such as symmetries and scale separation;

• Continuous-time formulations enabled by physics-based models inherit computational and other benefits; and

• They provide a compact, intuitive framework for probabilistic reasoning.

We provided numerous examples of the marriage of physics and AI, from energy-based models to diffusion models to Hamiltonian Monte Carlo to annealing-based optimization. We also pointed out some caveats like historical efforts that may exaggerate the impact of physics in AI. 

We thank you for taking the time to read this blog post! We hope this post stimulates discussion around the intersection of physics and AI. Be sure to sign up for updates at Normal Computing’s website.

Acknowledgments

We thank Anna Golubeva for helpful conversations and feedback.

References

[1] Sohl-Dickstein, J., Weiss, E., Maheswaranathan, N., & Ganguli, S. (2015, June). Deep unsupervised learning using nonequilibrium thermodynamics. In International Conference on Machine Learning (pp. 2256-2265). PMLR.

[2] Neal, R. M. (2011). MCMC using Hamiltonian dynamics. Handbook of markov chain monte carlo, 2(11), 2.

[3] Kirkpatrick, S., Gelatt Jr, C. D., Vecchi, M. P. (1983). Optimization by Simulated Annealing. Science. 220 (4598): 671–680.

[4] Fefferman, C., Mitter, S., Narayanan, H. (2016). Testing the manifold hypothesis. Journal of the American Mathematical Society. 29 (4): 983–1049.

[5] Liu, Z., Luo, D., Xu, Y., Jaakkola, T., Tegmark, M. (2023). GenPhys: From Physical Processes to Generative Models. arXiv preprint arXiv:2304.02637.

[6] Takeishi, N., Kalousis, A. (2021). Physics-integrated variational autoencoders for robust and interpretable generative modeling. Advances in Neural Information Processing Systems. 34: 14809–14821.

[7] Zehtabiyan-Rezaie, N., Iosifidis, A., Abkar, M. (2023). Physics-guided machine learning for wind-farm power prediction: Toward interpretability and generalizability. PRX Energy. APS. 2 (1): 013009.

[8] Chen, R. T. Q., Rubanova, Y., Bettencourt, J., Duvenaud, D. K. (2018). Neural ordinary differential equations. Advances in neural information processing systems. 31.

[9] Murphy, K. P. (2022). Probabilistic machine learning: an introduction. MIT press.

[10] Steinruecken, C., Smith, E., Janz, D., Lloyd, J., Ghahramani, Z. (2019). The automatic statistician. Automated machine learning: Methods, systems, challenges. Springer International Publishing. 161–173.

[11] Bronstein, M. M., Bruna, J., Cohen, T., Velickovic, P. (2021). Geometric deep learning: Grids, groups, graphs, geodesics, and gauges. arXiv preprint arXiv:2104.13478.

[12] O'Shea, K., Nash, R. (2015). An introduction to convolutional neural networks. arXiv preprint arXiv:1511.08458.

[13] Jumper, J. et al. (2021). Highly accurate protein structure prediction with AlphaFold. Nature. Nature Publishing Group UK London. 596 (7873): 583–589.

[14] Greydanus, S., Dzamba, M., Yosinski, J. (2019). Hamiltonian neural networks. Advances in neural information processing systems. 32.

[15] Cranmer, M., Greydanus, S., Hoyer, S., Battaglia, P., Spergel, D., Ho, S. (2020). Lagrangian neural networks. arXiv preprint arXiv:2003.04630.

[16] Wright, L. G., Onodera, T., Stein, M. M., Wang, T., Schachter, D. T., Hu, Z., McMahon, P. L. (2022). Deep physical neural networks trained with backpropagation. Nature. Nature Publishing Group UK London. 601 (7894): 549--555.

[17] Morris, E. R., Searle, M. S. (2012). Overview of protein folding mechanisms: experimental and theoretical approaches to probing energy landscapes. Current protocols in protein science. Wiley Online Library. 68 (1): 28–2.

[18] Ortega, P. A., Braun, D. A. (2013). Thermodynamics as a theory of decision-making with information-processing costs. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences. The Royal Society Publishing. 469 (2153): 20120683.

[19] LeCun, Y., Chopra, S., Hadsell, R., Ranzato, M., Huang, F. (2006). A tutorial on energy-based learning. Predicting structured data. 1 (0).

[20] Marullo, C., Agliari, E. (2020). Boltzmann machines as generalized Hopfield networks: a review of recent results and outlooks. Entropy. MDPI. 23 (1): 34.

[21] Song, Y., Sohl-Dickstein, J., Kingma, D. P., Kumar, A., Ermon, S., Poole, B. (2020). Score-based generative modeling through stochastic differential equations. arXiv preprint arXiv:2011.13456.

[22] Corso, G., Stärk, H., Jing, B., Barzilay, R., & Jaakkola, T. (2022). Diffdock: Diffusion steps, twists, and turns for molecular docking. arXiv preprint arXiv:2210.01776. 

[23] Wu, K. E., Yang, K. K., Berg, R. V. D., Zou, J. Y., Lu, A. X., & Amini, A. P. (2022). Protein structure generation via folding diffusion. arXiv preprint arXiv:2209.15611.

[24] Xie, T., Fu, X., Ganea, O. E., Barzilay, R., & Jaakkola, T. (2021). Crystal diffusion variational autoencoder for periodic material generation. arXiv preprint arXiv:2110.06197.

[25] Andrieu, C., De Freitas, N., Doucet, A., Jordan, M. I. (2003). An introduction to MCMC for machine learning. Machine learning. Springer. 50: 5–43.

[26] Chen, T., Fox, E., Guestrin, C. (2014). Stochastic gradient Hamiltonian Monte Carlo. International conference on machine learning. PMLR. 1683–1691.

[27] Camsari, K. Y., Sutton, B. M., & Datta, S. (2019). P-bits for probabilistic spin logic. Applied Physics Reviews, 6(1), 011305.

[28] Camsari, K. Y., Faria, R., Sutton, B. M., & Datta, S. (2017). Stochastic p-bits for Invertible Logic. Physical Review X, 7, 031014.

[29] Coles, P. J. (2023). Thermodynamic AI and the fluctuation frontier. arXiv preprint arXiv:2302.06584.

[30] Dao, Tri, Daniel Y Fu, Khaled K Saab, Armin W Thomas, Atri Rudra, and Christopher Ré. 2022. “Hungry Hungry Hippos: Towards Language Modeling with State Space Models.” arXiv Preprint arXiv:2212.14052.

[31] Liu, Chaoyue, and Mikhail Belkin. 2018. “Accelerating Sgd with Momentum for over-Parameterized Learning.” arXiv Preprint arXiv:1810.13395.