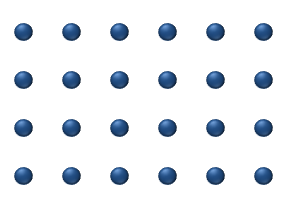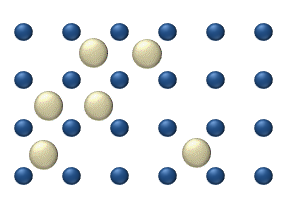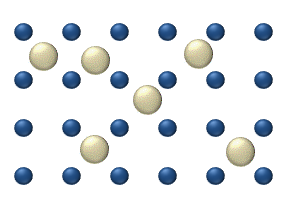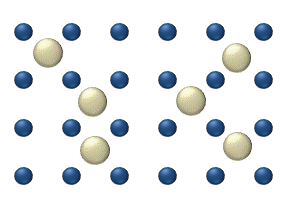Thermodynamic AI: intelligence from nature
Leveraging natural fluctuations may be the key to scaling AI that is capable of native, reliable reasoning
Overview
This blog post motivates a potential marriage between artificial intelligence (AI) and physics, especially thermodynamics. Furthermore, we discuss how building at this software and hardware intersection may be pre-requisite to democratizing fast, massively energy-efficient, and reliable AI.
Check out the pre-print for more! And join our mailing list to keep up with what we’re building at this intersection.
Thinking of AI algorithms from the perspective of physics has proven fruitful, and can allow one to unify seemingly unrelated algorithms (as we discuss below). Moreover, once AI algorithms are cast in the language of physics, one can design physics-based hardware to scale up such algorithms. Accordingly, in this blog, we build up to a full-stack paradigm that we believe will be crucial for achieving ubiquitous reliability in AI at the necessary problem (data and resource) scales.
At the heart of this full-stack is Thermodynamic AI hardware — a novel computing architecture based on fundamental building blocks that are inherently stochastic — and so casting AI software and hardware as inseparable[1] . In contrast to other paradigms like Quantum or Analog Computing, noise becomes a crucial resource for computation.
Beyond scaling up AI, we believe this new paradigm will also deepen our understanding of the connection between physics and intelligence.
Modern AI Algorithms
Modern AI has moved away from the absolute, deterministic procedures of early machine learning models. Nowadays, probability and randomness are fully embraced and utilized in AI. Some simple examples of this are avoiding overfitting by randomly dropping out neurons (i.e., dropout), and escaping local minima during training thanks to noisy gradient estimates (i.e., stochastic gradient descent). A deeper example is Bayesian neural networks[2], where the network’s weights are sampled from a probability distribution and Bayesian inference is employed to update the distribution in the presence of data, and so deal with data noise and uncertainty in principled fashion.
Another deep example is generative modeling with diffusion models[3]. Diffusion models add noise to data in a forward process, and then reverse the process to generate a new datapoint (see figure illustrating this for generating an image of a leaf). These models have been extremely successful not only in image generation, but also in generating molecules[4], proteins[5] and chemically stable materials[6].
AI is currently booming with breakthroughs largely because of these modern AI algorithms that are inherently random. At the same time, it is clear that AI is not reaching its full potential, because of a mismatch between software and hardware. For example, sample generation rate can be relatively slow for diffusion models[3], and Bayesian neural networks require approximations for their posterior distributions to generate samples in reasonable time[7]. There’s no inherent reason why digital hardware is well suited for modern AI, and indeed digital hardware is handicapping these exciting algorithms at the moment.
For production AI systems, Bayesianism in particular has been stifled from evolving beyond a relative niche because of its lack of mesh with digital hardware, despite general consensus regarding its benefits towards reliability. Indeed, today’s methods for leveraging Bayesian inference typically require exceptional mathematical sophistication given the highly technical literature around approximate (practical) Bayesian computation. Next generation production-ready software may be able to significantly reduce this gap in the near-term.
Nevertheless, the next hardware paradigm should be specifically tailored to the randomness in modern AI. Specifically, we must start viewing stochasticity as a computational resource. In doing so, we could build a hardware that uses the stochastic fluctuations produced by nature, and these fluctuations would naturally drive the computations necessary in modern AI applications. Let us now dive deeper into the building blocks of computing hardware to see what kind of hardware is needed for modern AI.
Building Blocks of Current Computers
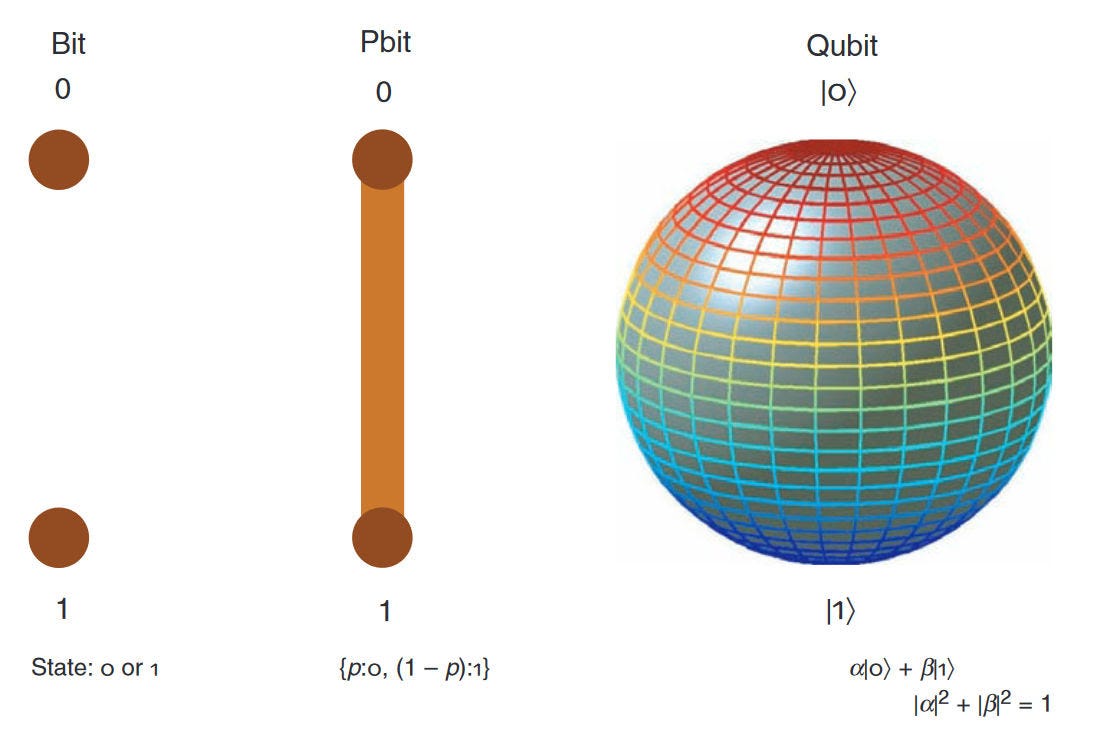
The invention of transistors led to digital computation, where the fundamental building block is the classical bit. At an abstract level, a bit can either be in the state 0 or 1. Recent decades have seen the introduction of novel building blocks that go beyond bits. See the figure below[8] for a comparison of bits with alternative paradigms.
Allowing the state space of a bit to be a continuum between 0 and 1 leads to probabilistic bits (p-bits)[9]. In p-bits, all convex combinations between 0 and 1 are allowed, with the coefficients being the probabilities of the p-bit holding value 0 or 1. Such p-bits are well suited to various applications such as optimization, Ising models[10], and other randomized algorithms. Magnetic tunnel junctions provide a potential hardware architecture for p-bits[9][11], as do Field-Programmable Gate Arrays (FPGAs)[12].
A further extension of state space allows for complex linear combinations of 0 and 1, that is, quantum superpositions. This extension is employed in quantum computers with the building block called a quantum bit or qubit. Qubits can be measured in different bases, with the complex square of the amplitudes in the linear combination giving the outcome probabilities. Qubits can be built from atoms, ions, electron spins, or superconducting circuits. Quantum computers[13][14] have tremendous promise for simulating quantum materials, designing pharmaceuticals, and analyzing quantum data.
One can see that there is a trend of moving closer towards physics-based computing, with both p-bits and qubits arguably being more physics-inspired than classical bits. Indeed, additional physics-based approaches have been developed for Boltzmann machines[15], combinatorial optimization[16] and neural networks[17] . In the same spirit as this trend, we introduce a new physics-inspired approach in what follows.
A New Building Block
The aforementioned building blocks are inherently static[18]. Ideally, the state does not change over time unless it is intentionally acted upon by a gate, in these paradigms.
However, modern AI applications involve accidental time evolution, or in other words, stochasticity. This raises the question of whether we can construct a building block whose state randomly fluctuates over time. This would be useful for naturally simulating the fluctuations in diffusion models, Bayesian inference, and other algorithms.
The key is to introduce a new axis when plotting the state space: time. Let us define a stochastic bit (s-bit) as a bit whose state stochastically evolves over time according to a continuous time Markov chain (CTMC). CTMC is a technical term for what is essentially a random jumping process in continuous time. We can then illustrate an s-bit by plotting the state versus time, as shown in the figure below.
However, there is no reason the fundamental building block needs to be a bit. In fact, most modern AI algorithms employ continuous spaces. For example, the weights in a neural network are continuous, and feature values of data are often continuous. This motivates our proposal of a continuous, stochastic building block.
Let us define a stochastic unit (s-unit) in an abstract sense as a real, continuous variable that undergoes Brownian motion, also known as a Wiener process in mathematics. The figure above shows how the state of an s-unit could evolve over time. We say that s-units are the fundamental building blocks of Thermodynamic AI hardware, which is the term we broadly use for this new hardware paradigm[19].
Ultimately this involves a shift in perspective. Certain computing paradigms, such as quantum and analog computing, view random noise as a nuisance. Noise is currently the biggest roadblock to realizing ubiquitous commercial impact for quantum computing. On the other hand, Thermodynamic AI views noise as an essential ingredient of its operation. Stochasticity is a valuable commodity[20], the key resource for Thermodynamic AI.
Physical Realization of Stochastic Units
An s-unit represents a continuous stochastic variable whose dynamics are governed by diffusion, drift, or drag (akin to a Brownian particle). At the heart of any physical implementation of such a variable will be a source of stochasticity. A natural starting point for implementing Thermodynamic AI hardware is analog electrical circuits[21], as these circuits have inherent fluctuations that could be harnessed for computation.
The most ubiquitous source of noise in electrical circuits is thermal noise, also called Johnson-Nyquist noise[22]. This noise comes from the random thermal agitation of the charge carriers in a conductor, resulting in fluctuations in voltage or current inside the conductor.
The s-unit can be represented through the dynamics of any degree of freedom of an electrical circuit (voltage, current, charge, etc.). If we choose the voltage on a particular node in a circuit as our degree of freedom of choice, we can implement an s-unit using a noisy resistor, illustrated in the following figure.
Here we modeled the noisy resistor as a combination of a stochastic voltage source (representing the thermal voltage fluctuations inside the noisy resistor), 𝛿v, an ideal noiseless resistor of resistance, R, and a capacitor of capacitance, C.
The stochastic dynamics of the s-unit in this circuit are constrained by the effect of the resistor and capacitor in the form of a drift (analogous to a force pushing a particle undergoing a random walk in a particular direction). In order for the s-units to be more expressive for computation, their inherent stochastic dynamics must be constrained to the properties of an algorithm. In general, one can add other electrical components, such as inductors or non-linear elements, to further constrain the evolution of the s-unit.
We note that one will need a means of coupling a system of s-units to generate correlations between them. There are a variety of options for this purpose, such as capacitive or resistive bridges that connect the s-units. Moreover, the bridges allow one to account for the geometry of the AI problem, and choosing a particular geometry for the couplings amounts to choosing an inductive bias for the AI model. In this sense, the couplings between s-units allow one to tailor the system to different problem geometries.
Unifying Algorithms via Thermodynamics
Let us now see why s-units are useful, but first we need to understand the common features that unify the AI algorithms of interest.
In physics, unifications are very powerful. For example, in the 19th century, James Clerk Maxwell unified three phenomena: electricity, magnetism, and light, under the same umbrella. Maxwell’s equations for electromagnetism showed that these seemingly unrelated phenomena were different aspects of one underlying physical force.
Our goal is to unify modern AI algorithms. The key to unifying these algorithms is recognizing similarities between them. Namely, many of them: (1) use stochasticity and (2) are inspired by classical physics. The branch of classical physics that involves stochasticity is known as Thermodynamics. Hence, it is natural to propose Thermodynamics as a field that could unify modern AI algorithms.
Since “modern” is a vague term, let us use the term Thermodynamic AI algorithms to describe the type of algorithms that we are interested in. Here we mention a few examples of Thermodynamic AI algorithms, although this is not a complete list:
Generative diffusion models
Hamiltonian Monte Carlo
Simulated Annealing
Note that each of these algorithms is physics-inspired. Generative diffusion models are inspired by classical diffusion, such as the Brownian motion of particles in a liquid or gas. Hamiltonian Monte Carlo[23], which is an algorithm sampling from a distribution, is inspired by Hamilton’s equation for position and momentum in classical mechanics. Simulated annealing is an optimization algorithm that is inspired by annealing in materials science, whereby heating and then cooling a material allows the atoms to rearrange so that the system progresses towards its equilibrium state.
Through careful consideration, one can formulate a mathematical framework that encompasses all of the aforementioned algorithms as special cases. Just as Maxwell proposed a system of differential equations to unify electromagnetism, we propose the following system of differential equations as being the fundamental equations of Thermodynamic AI algorithms:
For those who are versed in classical physics, these equations should look familiar. Here, p corresponds to the momentum vector, x is the position vector, f is the force vector, U is the potential energy function, and M is the mass matrix. The matrices B and D are hyper-parameters, e.g., D can be viewed as a diffusion matrix. The term dw represents Brownian motion (also known as a Wiener process), and hence this is the source of stochasticity. Note that these equations are essentially Newton’s laws of motion, with the addition of a friction term and a diffusion term. Mathematically, the first equation is a stochastic differential equation, the second is an ordinary differential equation, and the third is a partial differential equation.
We argue that the aforementioned algorithms are special cases of the above set of equations. In practice, essentially all of the application-specific information about the problem is encoded in the potential energy function U. In simulated annealing, U corresponds to the loss function that one would like to optimize. In Hamiltonian Monte Carlo, U is the logarithm of the probability distribution that one would like to sample from. In Diffusion Models, U is the logarithm of the noise-perturbed probability distribution (i.e., the data distribution with noise added).
The implications of this unification are significant. First, this unification implies that a single software view can be used to benchmark and implement all Thermodynamic AI algorithms. Second, and more importantly, it implies that a single hardware platform could be used to accelerate all such algorithms. Third, it implies that this hardware can be based on classical physics. Again, we call the latter: Thermodynamic AI hardware.
James Clerk Maxwell’s Demon
Let us give some intuition for how one can build this hardware based on classical physics. As one can imagine, the momentum vector p corresponds to the state variable of the stochastic units (s-units) described above, since p evolves according to a stochastic equation. But the s-units are only half the story.
We still need to introduce a system to evolve the position x in time, a system to compute the force f, and a system to apply the force as a drift term in the differential equation for p. It turns out that there is a system that can accomplish all of that, and it was introduced in the field of Thermodynamics once again by Maxwell. Maxwell considered an experiment where an intelligent observer monitors the gas particles in a box with two chambers and selectively opens the door for only fast moving particles, resulting in a separation of fast and slow particles over time (see figure). This reduces the entropy of the gas system over time, although it does not violate the 2nd law of thermodynamics since entropy is created elsewhere. The intelligent observer is dubbed Maxwell’s demon, and this demon has been experimentally realized in various physical systems[24][25], including electrical circuits[26].
The demon has the goal of separating the particles, and choosing this goal corresponds to choosing the application-specific potential energy function U. The demon computes the force f required and then applies it to the gas. One can therefore see that the device that we need in Thermodynamic AI is a Maxwell’s demon.
Going back to Thermodynamic AI algorithms, we can provide a simple, conceptual definition of such algorithms as one consisting of at least two subroutines:
(1) A subroutine in which a stochastic differential equation (SDE) is evolved over time.
(2) A subroutine in which a Maxwell's demon observes the state variable in the SDE and applies a drift term in response.
Hence, in addition to a physical device consisting of s-units, Thermodynamic AI hardware must also include a physical device corresponding to a Maxwell’s demon.
Computational Advantages Through Physics
Let us highlight three key subroutines where Thermodynamic AI hardware is expected to provide a speedup or advantage over standard digital computers for Thermodynamic AI algorithms:
Generating stochasticity: Simulating random noise on a digital device is somewhat unnatural; computers expend a significant amount of energy to prepare and keep deterministic states, which become the object of all computations, including those with random subroutines. In the language of physics, the computational state of a digital computer has zero-entropy throughout any program, even for the case of generating pseudo-random noise. In contrast, Thermodynamic AI hardware is driven by noisy physical systems that produce states with non-zero entropy. The s-unit system provides stochastic noise on demand, while digital hardware would need to expend computational effort to produce such noise. Given that Modern AI algorithms are hungry for stochasticity and entropy, Thermodynamic AI hardware can provide an advantage here.
Integrating dynamics: Stochastic differential equations are generally difficult to integrate digitally, as they can be numerically unstable especially in high dimensions, and they require careful scheduling of time step choices. With s-unit systems, on the other hand, there is no need to choose a time step and no instability, since the integration happens via physical evolution. In addition, digital approaches necessarily involve large matrix multiplications at every time step (e.g., computing BM-1p). In contrast, the physical evolution of s-units requires no matrix multiplications. Also, digital approaches would need to simultaneously evolve the differential equations for p and x as coupled equations. However, the physical approach taken by Thermodynamic AI hardware would have p and x corresponding to conjugate variables of the same physical system. These variables naturally evolve together over time in physical systems; this is known as phase space dynamics. For example, the figure below illustrates the phase space dynamics of a damped harmonic oscillator. Thus, no extra effort is needed to couple the p and x equations in physical systems, since they are naturally coupled.
Computing forces: A digital computer would need to compute the gradient of the potential energy at every time step in order to obtain the force f. In contrast, Thermodynamic AI hardware could, in principle, just measure this force instead of computing it. To elaborate, a physics-based Maxwell’s demon would essentially set up a (physical) potential energy surface U(x) for the position variable x. If we assume that x and p are conjugate variables of the same physical system, namely the s-unit system, then the Maxwell’s demon is tasked with setting up the potential energy surface for this s-unit system. But once this potential energy surface is set up, the dynamics of the s-unit system will naturally happen and the force (associated with the Maxwell’s demon) will naturally occur without any additional effort. In this sense, forces are an automatic byproduct of physical potential energy surfaces, i.e., they come for free. This is illustrated in the figure below.
A New Full-Stack Paradigm
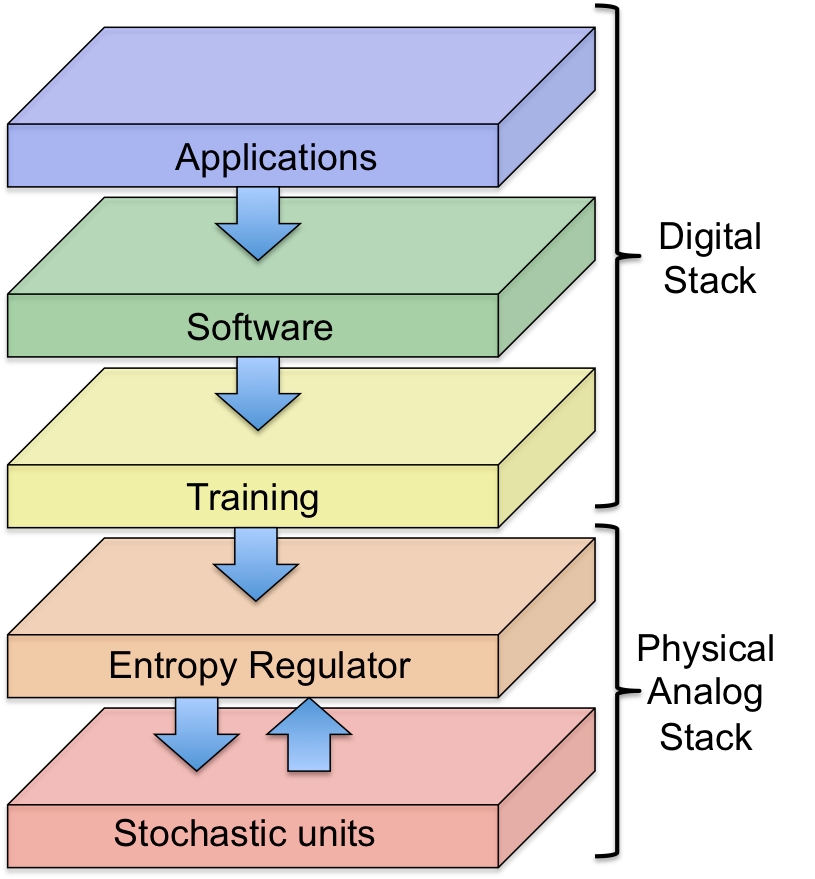
This brings us to the conclusion of this blog post. As a final remark, we mention a key technological implication of the above discussion: a single, unified, full-stack paradigm can be utilized for all Thermodynamic AI algorithms. Here is a simple schematic diagram for this full-stack perspective:
The stack is composed of a digital layer and a physical analog layer. At the top of the stack are applications and software, which will ultimately be used to program the hardware. Below the software layer is a training and optimization layer, whose job is to train the Entropy Regulator. Here we use the technical term Entropy Regulator in place of the casual term Maxwell’s demon that we used above. The Entropy Regulator is one component of the physical analog stack, and its job is to regulate the entropy of the stochastic unit system. The Entropy Regulator acts to guide the stochastic process in the right direction to solve the problem of interest. At the bottom of the stack is the stochastic unit system, which is analog hardware consisting of s-units evolving over time according to stochastic differential equations, as we describe above.
Conclusion
We hope this post stimulates discussion around Thermodynamic AI, including concepts like viewing stochasticity as a resource, and viewing AI algorithms from the lens of physics.
Stay tuned for more about how we’re building out this future at Normal Computing — join our waitlist for the Normal Computing AI platform!
References
[1] Hinton, G. (2022). The forward-forward algorithm: Some preliminary investigations. arXiv preprint arXiv:2212.13345.
[2] Goan, E., & Fookes, C. (2020). Bayesian neural networks: An introduction and survey. Case Studies in Applied Bayesian Data Science: CIRM Jean-Morlet Chair, Fall 2018, 45-87.
[3] Ho, J., Jain, A., & Abbeel, P. (2020). Denoising diffusion probabilistic models. Advances in Neural Information Processing Systems, 33, 6840-6851.
[4] Corso, G., Stärk, H., Jing, B., Barzilay, R., & Jaakkola, T. (2022). Diffdock: Diffusion steps, twists, and turns for molecular docking. arXiv preprint arXiv:2210.01776.
[5] Wu, K. E., Yang, K. K., Berg, R. V. D., Zou, J. Y., Lu, A. X., & Amini, A. P. (2022). Protein structure generation via folding diffusion. arXiv preprint arXiv:2209.15611.
[6] Xie, T., Fu, X., Ganea, O. E., Barzilay, R., & Jaakkola, T. (2021). Crystal diffusion variational autoencoder for periodic material generation. arXiv preprint arXiv:2110.06197.
[7] Izmailov, P., Vikram, S., Hoffman, M. D., & Wilson, A. G. G. (2021). What are Bayesian neural network posteriors really like?. International conference on machine learning, 4629-4640.
[8] Knill, E., Laflamme R., Barnum, H. N., Dalvit, D. A., Dziarmaga, J. J., Gubernatis, J. E., Gurvits, L., Ortiz, G., Viola, L., and Zurek, W. H. (2002). "Quantum Information Processing: A hands-on primer." Los Alamos Science, no. 27.
[9] Camsari, K. Y., Sutton, B. M., & Datta, S. (2019). P-bits for probabilistic spin logic. Applied Physics Reviews, 6(1), 011305.
[10] Chou, J., Bramhavar, S., Ghosh, S., & Herzog, W. (2019). Analog coupled oscillator based weighted Ising machine. Scientific reports, 9(1), 14786.
[11] Camsari, K. Y., Faria, R., Sutton, B. M., & Datta, S. (2017). Stochastic p-bits for Invertible Logic. Physical Review X, 7, 031014.
[12] Aadit, N. A., Grimaldi, A., Carpentieri, M., Theogarajan, L., Martinis, J. M., Finocchio, G., & Camsari, K. Y. (2022). Massively parallel probabilistic computing with sparse Ising machines. Nature Electronics, 5(7), 460-468.
[13] Preskill, J. (2012). Quantum computing and the entanglement frontier. arXiv preprint arXiv:1203.5813.
[14] Nielsen, M. A., & Chuang, I. L. (2011). Quantum Computation and Quantum Information: 10th Anniversary Edition. Cambridge University Press.
[15] Amin, M. H., Andriyash, E., Rolfe, J., Kulchytskyy, B., & Melko, R. (2018). Quantum boltzmann machine. Physical Review X, 8(2), 021050.
[16] King, A. D., Suzuki, S., Raymond, J., Zucca, A., Lanting, T., Altomare, F., ... & Amin, M. H. (2022). Coherent quantum annealing in a programmable 2,000 qubit Ising chain. Nature Physics, 18(11), 1324-1328.
[17] Wright, L. G., Onodera, T., Stein, M. M., Wang, T., Schachter, D. T., Hu, Z., & McMahon, P. L. (2022). Deep physical neural networks trained with backpropagation. Nature, 601(7894), 549-555.
[18] Some implementations of p-bits are inherently stochastic[9][11], although in this case, the stochasticity is not the end goal but rather a means to create a stream of random bits for p-bit construction.
[19] Stochastic fluctuations naturally occur in thermodynamics, and hence this explains our coining of the term Thermodynamic AI.
[20] Mansinghka, V. K. (2009). Natively Probabilistic Computation. Ph.D. Thesis, Citeseer.
[21] We remark that digital stochastic circuits were previously considered[20], although that differs from our analog approach.
[22] Horowitz, P., Hill, W., (2015). The art of electronics; 3rd ed.. Cambridge University Press.
[23] Neal, R. M. (2011). MCMC using Hamiltonian dynamics. Handbook of markov chain monte carlo, 2(11), 2.
[24] Vidrighin, M. D., Dahlsten, O., Barbieri, M., Kim, M. S., Vedral, V., & Walmsley, I. A. (2016). Photonic Maxwell’s demon. Physical review letters, 116(5), 050401.
[25] Lloyd, S. (1997). Quantum-mechanical Maxwell’s demon. Physical Review A, 56(5), 3374.
[26] Kish LB & Granqvist C.-G., (2012). Electrical Maxwell Demon and Szilard Engine Utilizing Johnson Noise, Measurement, Logic and Control. PLoS ONE 7(10): e46800.